上篇文章可加工陶瓷噴嘴的微鉆孔分析(五)
數值模型
在本節中,介紹了微型鉆的模態動態有限元分析和正交切削的有限元模型。
1.模態動態有限元分析
確定微型鉆頭的動態行為是選擇穩定切削參數的重要因素。通常,宏觀鉆頭的動力學是通過用沖擊錘激勵鉆頭并用加速度計測量工具尖端的位移來獲得的。耦合力和位移信號以獲得頻率響應函數。然后通過使用擬合技術獲得模態動態參數(模態阻尼、模態固有頻率、模態剛度和模態質量)。這種方法不能直接應用于微型鉆頭,因為加速度計不能連接到工具尖端。 FEA 出現作為獲得微型工具動力學的替代解決方案,其中可以考慮微型鉆頭的復雜幾何形狀。因此,本文使用 FEA 來獲得直徑為 100 μm 的微型鉆頭的動力學。

首先,對 CAD 幾何形狀和網格進行建模,以表示直徑為 100 μm 和槽長為 1.3 mm 的實際微型鉆頭。實際的微型鉆頭是通過 SEM 測量的,并相應地生成 FE 網格(見圖 6)。微型鉆頭采用積分減少的二次四面體單元進行網格劃分。假設涂層薄層不影響刀具動力學,并且微型鉆頭被建模為彈性模量為 580 GPa、泊松比為 0.28 且密度為 14,300 kg/m3 的碳化物材料。零位移應用于與夾頭接觸的柄節點。動態 FEA 分兩步執行。在第一步中,使用 Lanczos 特征求解器執行頻率分析以獲得 0-10 KHz 范圍內頻率的模式形狀。模態分析在步驟 2 中通過考慮來自頻率分析的預測模態形狀來執行。在模態分析步驟中,集中力施加在兩個工具尖端以表示扭矩。此外,在軸向上施加集中力。在模態動態分析中不考慮阻尼,因為主要目的是獲得微型鉆頭振動的固有頻率。
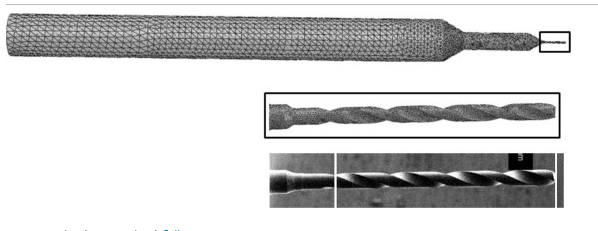
圖 6. 直徑為 100 μm 的微型鉆頭的 FE 網格和 SEM 圖像
2.正交切削的有限元模型
正交切削的有限元模型已廣泛用于預測各種切削操作中的切削力、切屑形成和殘余應力。例如,正交切削的預測切削力可能與微觀和宏觀尺度的車削、拉削和銑削操作相關。在鉆孔中,正交切削只能代表切削刃處的切削機理。它還可以預測作用在切削刃上的切削力,但不能預測鑿唇、摩擦和去除材料的疏散的影響。正交切割的有限元建模可用于描述 Macor 的切割機制,其中可以做出一些工程決策。

使用 Afazov 等人開發的顯式積分模型在動態熱機械 FEA 中模擬 Macor 的正交切割。 (2010)。在 FE 模型中,工具的幾何形狀是根據掃描電子顯微鏡測量結果創建的。對于直徑為 100 μm 的 2 個雙刃 TiN 涂層微型鉆頭,使用 SEM 測量的邊緣半徑約為 0.8 μm(見圖 7)。刀具和工件之間采用滑粘摩擦模型。應該提到的是,由于接觸壓力的變化,摩擦會導致切削力的非線性。例如,邊緣半徑會產生更高的接觸壓力,而摩擦會導致粘附占主導地位的行為。根據 McKellop 等人進行的實驗研究,選擇了 0.1 的摩擦系數。 (1981)。研究報告稱,Macor 具有低摩擦系數。第 3 節中描述的材料模型在 FE 模型中實現。有限元模型與線性四邊形單元網格化,集成度降低,接觸區域的尺寸約為 5 nm。一旦達到損壞標準,這些單元就會從剛度矩陣中停用。表 2 給出了正交切削有限元模型中使用的 Macor 機械和物理特性。

圖7微鉆的 SEM 圖像和測量的切削刃半徑

表 2. Macor 的機械和物理材料特性
(MACOR是由康寧公司生產的可加工陶瓷)